Смешанное соединение резисторов формула

Смешанное соединение резисторов. Расчет смешанного соединения

Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.

В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.

Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.

И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.

Расчет смешанного соединения резисторов.

Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.

Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.

Разберем схему смешанного соединения из семи резисторов:

Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:

Вычисляем их общее сопротивление используя формулу параллельного соединения:

Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.

Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:

Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):

Схема уменьшилась еще на один элемент и приняла вид:

Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:

Вычисляем их общее сопротивление:

Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.

Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:

Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

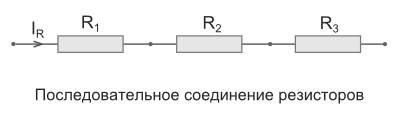
Общее сопротивление R_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

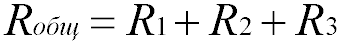
Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

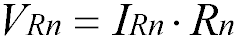
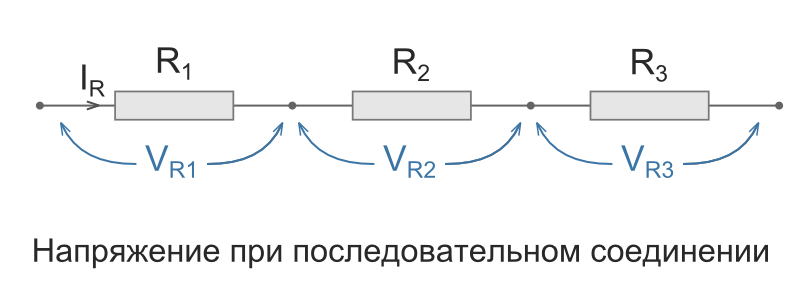
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

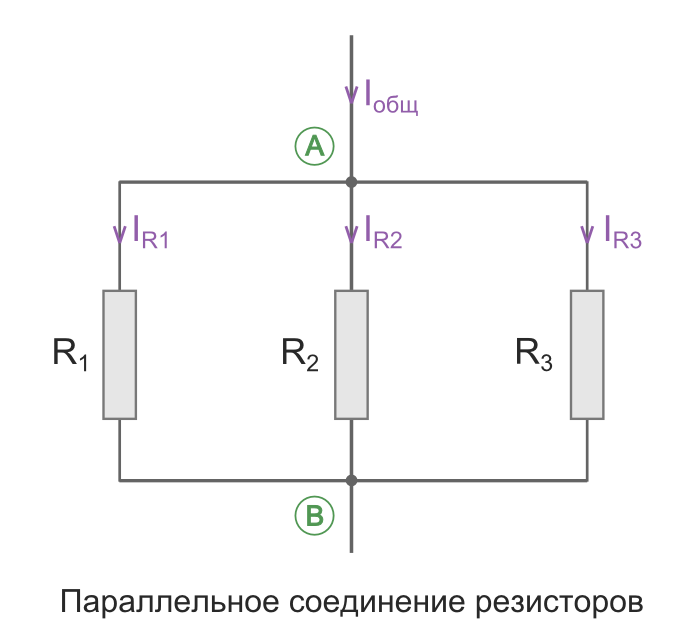
Общее сопротивление R_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

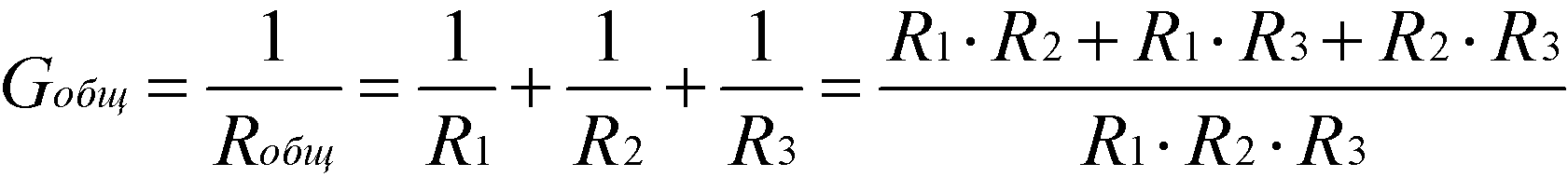
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

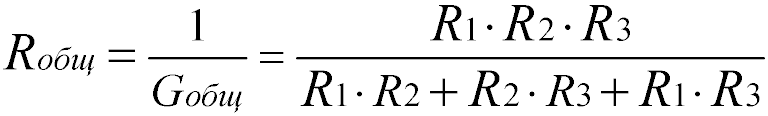
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

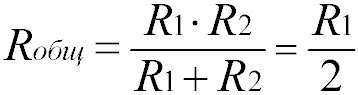
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

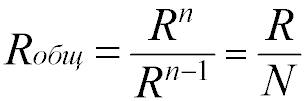
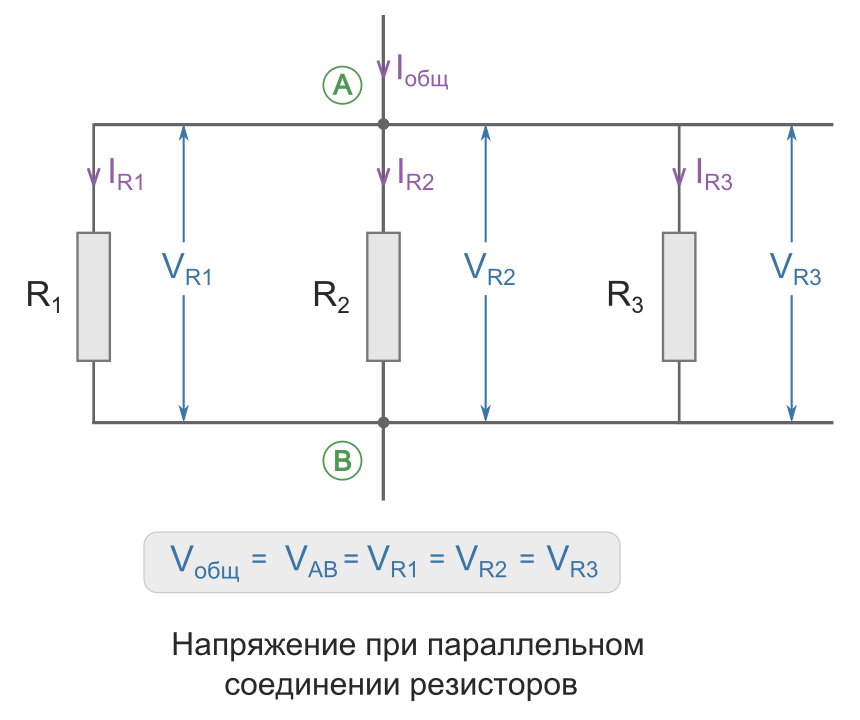
Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

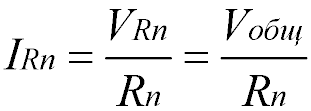
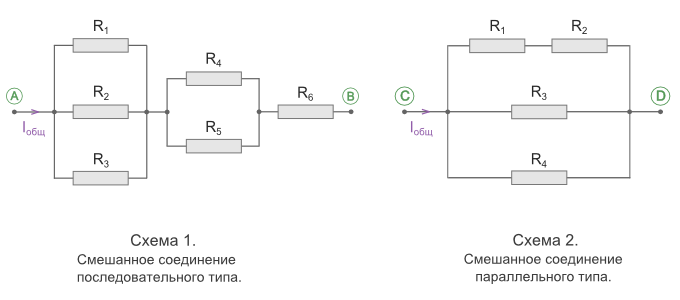
Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

• Цепь разбивают на участки с только пареллельным или только последовательным соединением.
• Вычисляют общее сопротивление для каждого отдельного участка.
• Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

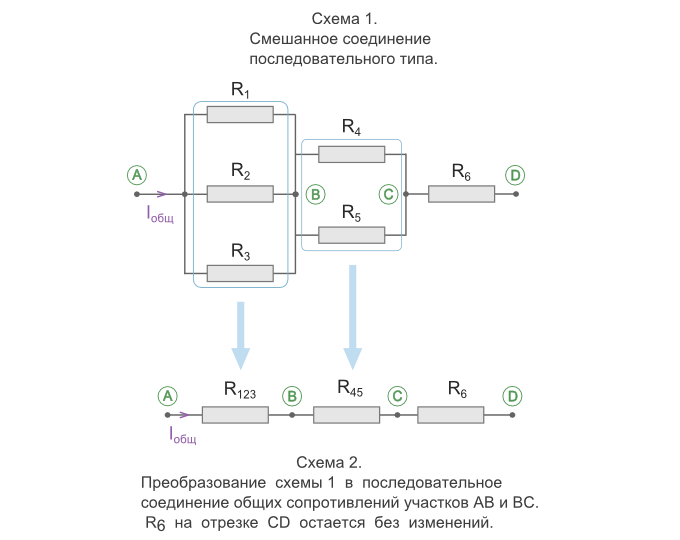
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

• Если резисторы соединяются последоватеьно — складывать.
• Если резисторы соединяются параллельно — использовать условное обозначение «||».
• Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Смешанное соединение сопротивлений

Электрические цепи, в которых одна часть сопротивлений соединена последовательно, а другая параллельно, называются цепями со смешанным соединением сопротивлений.

Общих расчетных формул для таких цепей нет, так как число их разновидностей не ограничено.

Чаще всего расчет подобных схем начинается с определения эквивалентного сопротивления всей цепи, а затем определяются величины токов и падение напряжения на отдельных участках.

Для определения эквивалентного сопротивления цепи со смешанным соединением потребителей, питающихся от одного источника тока, необходимо прежде всего разбить эту цепь на отдельные участки, состоящие из последовательного и параллельно соединенных сопротивлений. Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.

Рассмотрим метод решения задач на смешанное соединение сопротивлений на конкретном примере.

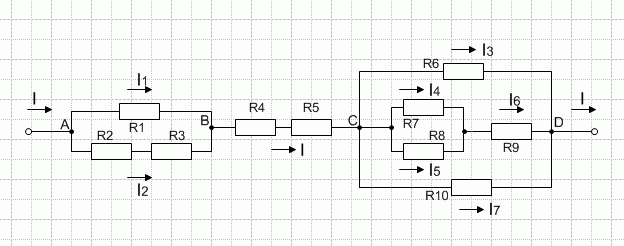
На рисунке представлена схема смешанного соединения сопротивлений. Ее можно разбить на три участка:

участок АВ – с двумя параллельно соединенными ветвями;

участок ВС – с последовательно соединенными сопротивлениями;

участок СD – с тремя параллельными ветвями.

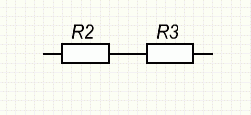
Кроме того, нижняя ветвь участка АВ представляет в свою очередь цепь, состоящую из двух последовательно соединенных сопротивлений R₂ и R₃.

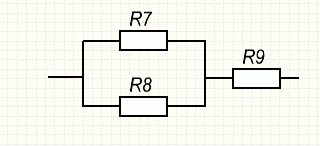
Центральная ветвь участка СD представляет собой смешанное соединение сопротивлений.

Расчет данной сложной цепи надо начинать с определения R_экв для нижней ветви участка АВ и центральной ветви участка СD.

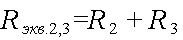
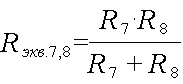
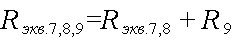
Теперь мы можем упростить первоначальную схему. Она будет иметь следующий вид

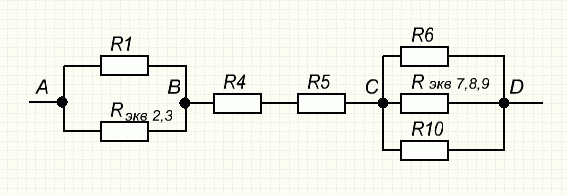
Определим эквивалентные сопротивления каждого из участков:

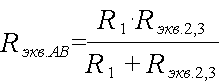
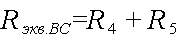
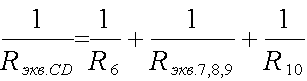
После этих вычислений можно продолжить упрощение схемы

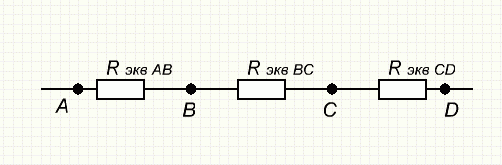
Полученная упрощенная схема, состоящая в данном случае из трех последовательно соединенных сопротивлений, называется по отношению к реальной эквивалентной схемой.

Определим R_экв всей цепи как сумму трех последних сопротивлений

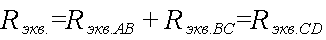
Зная напряжение источника тока, применяя формулу закона Ома, определим ток в не разветвленном участке смешанной цепи

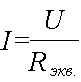
Определив величину тока, найдем падение напряжения на участках эквивалентной схемы АВ, ВС, CD:

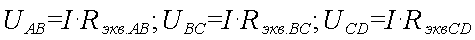
Теперь можно определить токи в параллельных ветвях участков АВ и СD

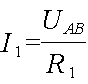
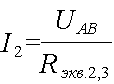
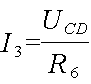
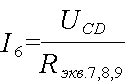
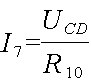
Остается определить величину токов, протекающих через сопротивления R₇ и R_8. Для этого надо сначала определить падение напряжения на сопротивлениях R₇ и R_8.

Определим падение напряжения на сопротивлении R₉:

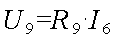
Падение напряжения на сопротивлении R_7,8 определится как разность U_CD и U:

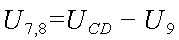
Теперь определим величины токов, протекающих через сопротивления R₇ и R₈:

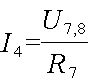
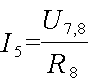
Величина тока. протекающего через сопротивления R₄ и R₅, равна I – току в неразветвленном участке цепи.

Итак, при решении задач на смешанное соединение сопротивлений необходимо, постепенно упрощая схему, определить эквивалентное сопротивление всей цепи, а затем. восстанавливая постепенно реальную схему. вычислить падение напряжения и токи в отдельных ветвях.

Смешанное соединение сопротивлений

Эквивалентное сопротивление цепи.

Пример 1.1. Цепь постоянного тока со смешанным соединением состоит из четырёх резисторов. Мощность электрической цепи Р = 750 Вт. Определить эквивалентное сопротивление цепи, токи и напряжения на всех резисторах и для всей цепи. Решение проверить, используя баланс мощностей.

(Указание: номера токов, напряжений и мощностей должны совпадать номерами сопротивлений.)

Дано: R₁=10 Ом; R₂ = 50 Ом; R₃ = 40 Ом; R₄= 6 Ом; Р = 750 Вт.

Определим эквивалентное сопротивление цепи методом свёртывания.

Если между сопротивлениями нет узла, то они соединены последовательно, а между двумя узлами имеется параллельное соединение сопротивлений.

R₁ и R₂ соединены последовательно, R₁₂ и R₃ параллельно, а R₁₂₃ и R₄ последовательно.

R = R₁₂₃ + R₄ = 24 + 6 = 30 Ом.

Определим токи и напряжения на всех резисторах.

Ток и напряжение для всей цепи:

Рис. 1.9. получается свёртыванием рис. 1.8. На рисунке 1.10 покажем токи и напряжения на резисторах R₁₂₃ и R₄:

Решение проверим, используя 2-ой закон Кирхгофа.

U = U₃ + U₄ = 120 + 30 = 150 В.

Резистор R₁₂₃ получается от параллельного соединения резисторов R₁₂ и R₃.

Из рис. 1.11. имеем:

Решение проверим, используя 1-ый закон Кирхгофа.

Резистор R₁₂ получается от последовательного соединения резисторов

Решение проверим, используя 2 – ой закон Кирхгофа.

150 · 5 =20 · 2 + 100 · 2 + 120 · 3 + 30 · 5 = 40 + 200 + 360 + 150 = 750;

Ответ представим в виде таблицы:

Задача 1.1. Цепь постоянного тока со смешанным соединением состоит из четырёх резисторов. Дана одна из величин U,I или Р. Определить эквивалент- ное сопротивление цепи, токи и напряжения на всех резисторах и для всей цепи. Решение проверить, используя баланс мощностей.

(Указание: номера токов, напряжений и мощностей должны совпадать номерами сопротивлений.) Данные выбрать из таблицы 1.1.

Пример 1.2.Дана электрическая цепь со смешанным соединением резисторов. Номера токов, напряжений и мощностей совпадают с номером резистора.

1.эквивалентное сопротивление электрической цепи;

2.используя известную величину тока, напряжения или мощности вычис-

лить токи и напряжения, по закону Ома для участка цепи, на всех резис-

торах и для всей цепи; законы Кирхгофа использовать для проверки;

3.проверить решение методом баланса мощностей.

Для определения эквивалентного сопротивления используем метод свёртывания.

R₅ и R₆ cоединены параллельно, а R₄ и R₅₆ последовательно.

R₃ и R₄₅₆ cоединены параллельно, R₁ и R₂ c R₃₄₅₆ последовательно.

Определим ток и напряжение всей цепи:

Из рис. 1.26 видим, что резисторы R₁, R₃₄₅₆, R₂ соединены последовательно,

определим напряжения и токи на R₁, R₃₄₅₆, R₂. На рис.1.27 покажем токи и напряжения.

Проверим используя 2-ой закон Кирхгофа.

U = U₁ + U₃ + U₂ ; 50 = 5 + 30 + 15 = 50

Рассмотрим резистор R₃₄₅₆. Выделим из рис. 1.25. часть с резисторами R₃ и R₄₅₆, получим рис.1.28. Ток I₄₅₆ равен I₄ т.е. I₄₅₆ = I₄. Определим токи I₄ и I₁. Из рис. 1.28 видно: напряжение U₄₅₆ = U₃ т.к. R₃ и R₄₅₆ соединены параллельно. Токи в ветвях:

Проверим, используя 1-ый закон Кирхгофа.

Отделим из рис.1.24 резисторы R₄ и R₅₆. Эти резисторы соединены последовательно. На рис. 1.29 покажем напряжения U₄ и U₅₆ = U₅ = U₆.

Проверим используя 2-ой закон Кирхгофа.

Из рис.1.23 видим, что резисторы R₅ = R₆ соединены параллельно. На рис.1.30 покажем токи I₅ и I₆. Определим токи на резисторах R₅ и R₆ .

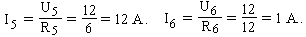
Проверим используя 1-ый закон Кирхгофа: I₄= I₅ + I₆; 3 = 2 + 1.

Из рис.1.30 определим напряжения на R₁ и R₂: I = I₁ = I₂ = I₃₄₅₆ = 5 А.

Решение проверим используя баланс мощностей:

50·5 = 5·5 + 15·5 + 30·2 + 18·3 + 12·2 + 12·2 = 250.

Задача 1.2.Дана электрическая цепь со смешанным соединением резисто- ров. Номера токов, напряжений и мощностей совпадают с номером резистора. Данные выбрать из таблицы 1.2.

Определить используя заданную величину U,I, или Р:

1.Эквивалентное сопротивление электрической цепи.

2.Используя известную величину тока, напряжения или мощности вычислить токи и напряжения, по закону Ома для участка цепи, на всех резисторах и для всей цепи. Законы Кирхгофа использовать для проверки.

3. Решение проверить методом баланса мощностей.